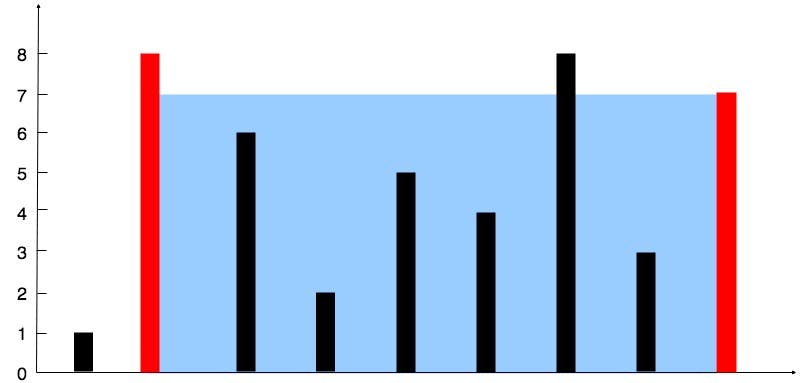
Problem Description

Given n non-negative integers a1, a2, ..., an, where each represents a point at coordinate (i, ai). n vertical lines are drawn such that the two endpoints of the line i is at (i, ai) and (i, 0). Find two lines, which, together with the x-axis forms a container, such that the container contains the most water.

Notice that you may not slant the container.

Link to the problem: https://leetcode.com/problems/container-with-most-water/

Solution

We can solve this problem using the Two-Pointer Approach. We will initialize two pointers, one at the beginning and one at the end of the array, and calculate the area between them. We will then move the pointer with the smaller height and repeat the same process until the pointers meet.

class Solution:
    def maxArea(self, height: List[int]) -> int:
        left = 0
        right = len(height) - 1
        max_area = 0

        while left < right:
            area = min(height[left], height[right]) * (right - left)
            max_area = max(max_area, area)

            if height[left] < height[right]:
                left += 1
            else:
                right -= 1

        return max_area

In the above code, we initialize the left and right pointers to the beginning and end of the array respectively. We also initialize the max_area to 0.

We then calculate the area between the two pointers using the formula min(height[left], height[right]) * (right - left) and update the max_area if the calculated area is greater than the current max_area.

We then move the pointer with the smaller height. If the height at the left pointer is smaller, we move the left pointer one step to the right, else we move the right pointer one step to the left.

We continue this process until the pointers meet and return the max_area.

Complexity Analysis

The time complexity of this solution is O(n) as we are iterating through the array only once. The space complexity is O(1) as we are using constant space.

Conclusion

We have successfully solved the Container With Most Water problem using the Two-Pointer Approach. This approach is a very efficient way of solving problems where we need to find a pair of elements satisfying some conditions. Happy Coding! 😎